What is Percentage Impedance in Dry Type Transformers
Definition of Percentage Impedance
Percentage impedance, denoted as %Z, is a critical parameter in dry type transformers that represents the internal resistance of the transformer windings to alternating current. It is expressed as a percentage of the transformer’s rated voltage and determines the transformer’s ability to limit short-circuit currents. The impedance value is a combination of the transformer’s resistance and reactance, which are influenced by factors such as the winding material, cross-sectional area, number of turns, and the spacing between windings.
A transformer’s percentage impedance directly affects its performance, including short-circuit current, voltage regulation, and efficiency. A higher percentage impedance results in lower fault currents, providing better protection for the transformer and the connected electrical system. However, a higher impedance also leads to larger voltage drops from no-load to full-load conditions, impacting voltage regulation. Additionally, higher impedance values increase winding losses, reducing the transformer’s overall efficiency.
Typical Percentage Impedance Values for Dry Type Transformers
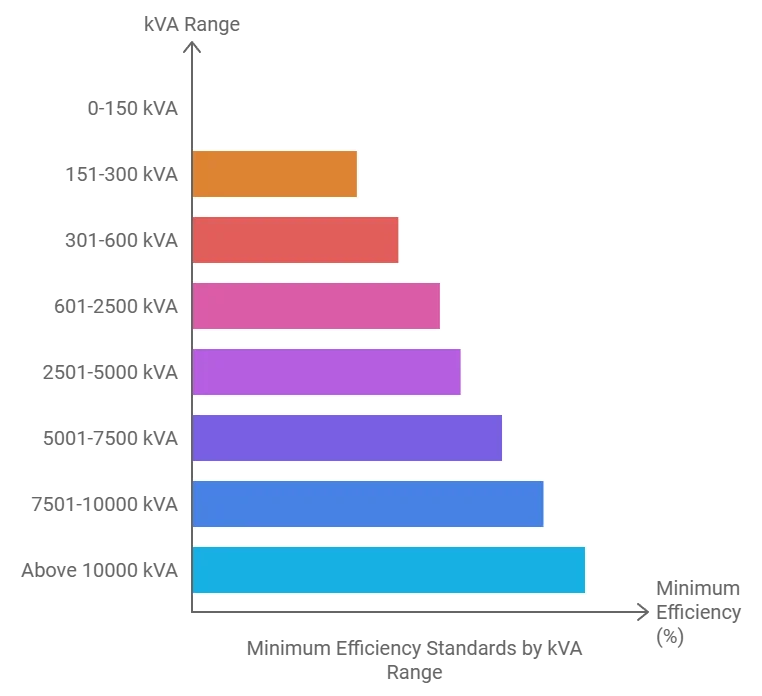
Impedance Levels by kVA Rating
- 0-150 kVA: Manufacturer’s standard
- 151-300 kVA: 4% minimum
- 301-600 kVA: 5% minimum
- 601-2500 kVA: 6% minimum
- 2501-5000 kVA: 6.5% minimum
- 5001-7500 kVA: 7.5% minimum
- 7501-10000 kVA: 8.5% minimum
- Above 10000 kVA: 9.5% minimum
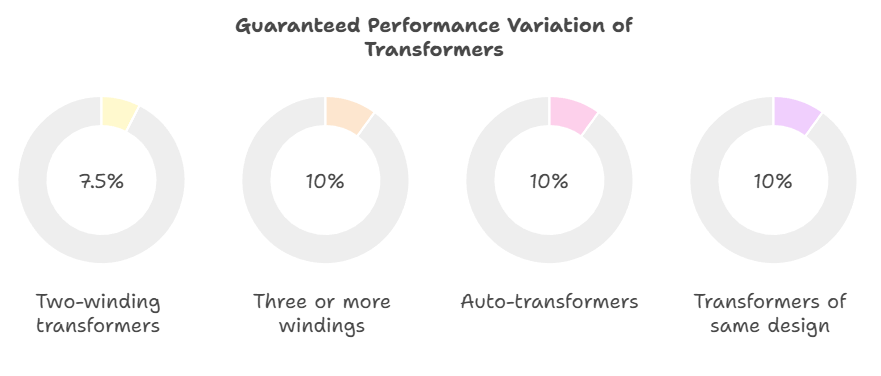
Allowable Tolerances
- Two-winding transformers: ±7.5% of guaranteed value
- Three or more windings: ±10% of guaranteed value
- Auto-transformers: ±10% of guaranteed value
- Transformers of same design: Differences shall not exceed 10% of guaranteed values
Measuring Percentage Impedance
Percentage Impedance (Z%) = (Impedance Voltage / Rated Primary Voltage) x 100
Example Calculation:
2400/240V transformer with impedance voltage of 72V
Z% = (72V / 2400V) x 100 = 3%
Impact on Transformer Performance
Short Circuit Current
Percentage impedance plays a crucial role in determining the short circuit current of a dry type transformer. A higher impedance value results in lower fault currents, which can be beneficial for protecting the transformer and the connected electrical system during short circuit events. The relationship between fault current and percentage impedance can be expressed using the following formula:
Fault Current = Rated Secondary kVA / (√3 x %Z x Rated Secondary Voltage)
For example, consider a 500 kVA dry type transformer with a rated secondary voltage of 480V and a percentage impedance of 5%. Using the formula above, the fault current would be:
Fault Current = 500,000 VA / (√3 x 0.05 x 480V) ≈ 12,000A
This demonstrates how a higher percentage impedance can limit the fault current, reducing the potential damage to the transformer and the connected electrical system during short circuit conditions.
Voltage Regulation
Voltage regulation refers to the transformer’s ability to maintain a constant secondary voltage under varying load conditions. A higher impedance causes a larger voltage drop from no-load to full-load, resulting in poorer voltage regulation.
The voltage drop across the transformer’s impedance is proportional to the load current. As the load increases, the voltage drop becomes more significant, leading to a lower secondary voltage at full-load compared to no-load conditions. This voltage drop can be calculated using the following formula:
Voltage Drop = Load Current x Impedance
Efficiency
The efficiency of a dry type transformer is influenced by its percentage impedance. Higher impedance values increase the winding losses, which are the resistive losses in the transformer’s primary and secondary windings. These losses are proportional to the square of the load current and are dissipated as heat.
Winding Losses = I^2 x R
Where I is the load current, and R is the winding resistance.
As the percentage impedance increases, the winding resistance also increases, leading to higher winding losses and reduced transformer efficiency. This is particularly significant under high load conditions, where the load current is substantial.



